MHD equations

The magnetospheric part of GUMICS is based on the conservative formulation of the magnetohydrodynamic (MHD) equations. They are discretised and solved using a first order finite volume method.

The primary variables

The primary variables of GUMICS are:

ρ, mass density
p = ρv, momentum density
U₁, total energy density excluding dipole
B₁, magnetic field excluding dipole

The magnetic field is treated as a sum of an analytically calculated dipole field and a deviation field, B = B₀ + B₁. Correspondingly, the large dipole contribution is separated from the total energy density, U = U₀ + U₁.

The benefit of splitting the magnetic field and the total energy density to dipole contribution and deviation is that when calculating the pressure, one does not need to subtract from U the dipole contribution B₀² / (2μ₀), which is very large close to the Earth. This reduces numerical error and makes it easier to maintain positive pressure. With the splitted quantities the pressure is calculated as P = (γ − 1)(U₁ − p²/(2ρ) − B₁²/(2μ₀)).

All other MHD plasma variables can be derived from the primary ones. Therefore the simulation only solves and saves the values of the primary variables, and other quantities are calculated from them as post-processing variables when required for analysis.

The equations

With the above given variables, the MHD equations are:

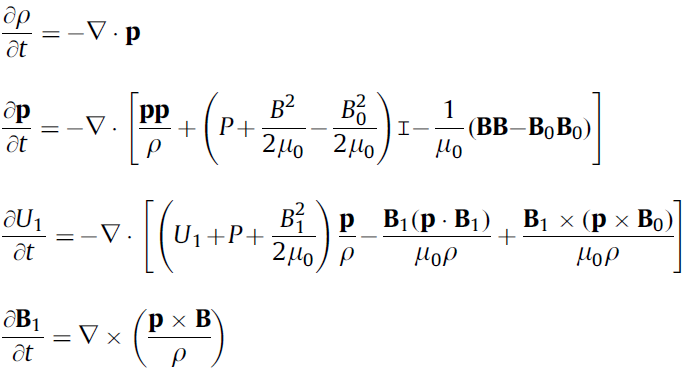
These equations can be interpreted as:

Conservation of mass
Newton's second law, with pressure gradient and Lorentz' force as force terms
Conservation of energy
Faraday's law.

Numerical solvers

The MHD equations are discretised and solved using first order finite volume methods. Each cell stores the volume average of the quantities within, and solvers solve for fluxes through the cell surfaces, which are then added to the cell contents.

The primary solver is Roe's approximate Riemann solver (Roe, 1981). However, this solver may produce unphysical intermediate states with negative density or pressure. In case this happens, the Roe solution is discarded and the more diffusive but always physical Harten–Lax–-van Leer solver (Harten et al. 1983) is used instead for that cell interface and timestep.

References

Roe, P.L., 1981. Approximate Riemann solvers, parameter vectors, and difference schemes. Journal of Computational Physics 43, 357–372.
Harten, A., Lax, P.D., van Leer, B., 1983. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Review 25, 35–61.